NBA数据分析初探(上)
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns #%matplotlib inline ##魔法命令了解一下, 内嵌画图 是IPython的内置magic函数,那么在Pycharm中是不会支持的。 #载入数据: data=pd.read_csv('D:/pycharm_ngs_programs/data_analysis/nba_2017_nba_players_with_salary.csv') print(data.head(5)) ## 描述统计 print(data.shape) print(data.describe())
输出结果如下:
Unnamed: 0 Rk PLAYER POSITION AGE MP FG FGA FG% \ 0 0 1 Russell Westbrook PG 28 34.6 10.2 24.0 0.425 1 1 2 James Harden PG 27 36.4 8.3 18.9 0.440 2 2 3 Isaiah Thomas PG 27 33.8 9.0 19.4 0.463 3 3 4 Anthony Davis C 23 36.1 10.3 20.3 0.505 4 4 6 DeMarcus Cousins C 26 34.2 9.0 19.9 0.452 3P ... GP MPG ORPM DRPM RPM WINS_RPM PIE PACE \ 0 2.5 ... 81 34.6 6.74 -0.47 6.27 17.34 23.0 102.31 1 3.2 ... 81 36.4 6.38 -1.57 4.81 15.54 19.0 102.98 2 3.2 ... 76 33.8 5.72 -3.89 1.83 8.19 16.1 99.84 3 0.5 ... 75 36.1 0.45 3.90 4.35 12.81 19.2 100.19 4 1.8 ... 72 34.2 3.56 0.64 4.20 11.26 17.8 97.11 W SALARY_MILLIONS 0 46 26.50 1 54 26.50 2 51 6.59 3 31 22.12 4 30 16.96 [5 rows x 39 columns] Unnamed: 0 Rk AGE MP FG FGA \ count 342.000000 342.000000 342.000000 342.000000 342.000000 342.000000 mean 170.500000 217.269006 26.444444 21.572515 3.483626 7.725439 std 98.871128 136.403138 4.295686 8.804018 2.200872 4.646933 min 0.000000 1.000000 19.000000 2.200000 0.000000 0.800000 25% 85.250000 100.250000 23.000000 15.025000 1.800000 4.225000 50% 170.500000 205.500000 26.000000 21.650000 3.000000 6.700000 75% 255.750000 327.750000 29.000000 29.075000 4.700000 10.400000 max 341.000000 482.000000 40.000000 37.800000 10.300000 24.000000 FG% 3P 3PA 3P% ... \ count 342.000000 342.000000 342.000000 320.000000 ... mean 0.446096 0.865789 2.440058 0.307016 ... std 0.078992 0.780010 2.021716 0.134691 ... min 0.000000 0.000000 0.000000 0.000000 ... 25% 0.402250 0.200000 0.800000 0.280250 ... 50% 0.442000 0.700000 2.200000 0.340500 ... 75% 0.481000 1.400000 3.600000 0.373500 ... max 0.750000 4.100000 10.000000 1.000000 ... GP MPG ORPM DRPM RPM WINS_RPM \ count 342.000000 342.000000 342.000000 342.000000 342.000000 342.000000 mean 58.198830 21.572807 -0.676023 -0.005789 -0.681813 2.861725 std 22.282015 8.804121 2.063237 1.614293 2.522014 3.880914 min 2.000000 2.200000 -4.430000 -3.920000 -6.600000 -2.320000 25% 43.500000 15.025000 -2.147500 -1.222500 -2.422500 0.102500 50% 66.000000 21.650000 -0.990000 -0.130000 -1.170000 1.410000 75% 76.000000 29.075000 0.257500 1.067500 0.865000 4.487500 max 82.000000 37.800000 7.270000 6.020000 8.420000 20.430000 PIE PACE W SALARY_MILLIONS count 342.000000 342.000000 342.000000 342.000000 mean 9.186842 98.341053 28.950292 7.294006 std 3.585475 2.870091 14.603876 6.516326 min -1.600000 87.460000 0.000000 0.030000 25% 7.100000 96.850000 19.000000 2.185000 50% 8.700000 98.205000 29.000000 4.920000 75% 10.900000 100.060000 39.000000 11.110000 max 23.000000 109.870000 66.000000 30.960000 [8 rows x 36 columns]
从数据中看几项比较重要的信息:
-
球员平均年龄为26.4岁,年龄段在19-38岁;
-
球员平均年薪为730万美金,当时最大的合同为年薪3000万美金;
-
球员平均出场时间为21.5分钟,某球员场均出场37.8分钟领跑联盟,当然也有只出场2.2分钟的角色球员,机会来之不易。
-
类似的信息我们还能总结很多。
效率值相关性分析
在众多的数据中,有一项名为“RPM”,标识球员的效率值,该数据反映球员在场时对球队比赛获胜的贡献大小,最能反映球员的综合实力。
我们来看一下它与其他数据的相关性:
dat_cor=data.loc[:,['RPM','AGE','SALARY_MILLIONS','ORB','DRB','TRB','AST','STL','BLK','TOV','PF','POINTS','GP','MPG','ORPM','DRPM']] coor=dat_cor.corr() sns.heatmap(coor,square=True, linewidths=0.02, annot=False) #seaborn中的heatmap函数,是将多维度数值变量按数值大小进行交叉热图展示。

由相关性分析的heatmap图可以看出,RPM值与年龄的相关性最弱,与“进攻效率值”、“场均得分”、“场均抢断数”等比赛技术数据的相关性最强。
我在接下来的分析中将把RPM作为评价一个球员能力及状态的直观反应因素之一。
球员数据分析部分
此处练习了一下pandas基本的数据框相关操作,包括提取部分列、head()展示、排序等,简单通过几个维度的展示,笼统地看一下16-17赛季那些球员冲在联盟的最前头。
data.loc[:,['PLAYER','SALARY_MILLIONS','RPM','AGE','MPG']].sort_values(by='SALARY_MILLIONS',ascending=False).head(10) #效率值最高的10名运动员 data.loc[:,['PLAYER','RPM','SALARY_MILLIONS','AGE','MPG']].sort_values(by='RPM',ascending=False).head(10) #出场时间最高的10名运动员 data.loc[:,['PLAYER','RPM','SALARY_MILLIONS','AGE','MPG']].sort_values(by='MPG',ascending=False).head(10)
结果如下: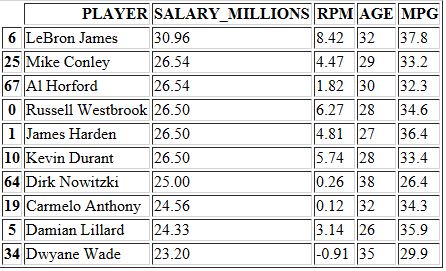


Seaborn常用的三个数据可视化方法
单变量:
distplot方法可以绘制直方图和连续密度估计,通过distplot方法seaborn使直方图和密度图的绘制更为简单,
我们先利用seaborn中的distplot绘图来分别看一下球员薪水、效率值、年龄这三个信息的分布情况,代码如下:
#单变量: #我们先利用seaborn中的distplot绘图来分别看一下球员薪水、效率值、年龄这三个信息的分布情况,上代码: #分布及核密度展示 sns.set_style('darkgrid') #设置seaborn的面板风格 plt.figure(figsize=(12,12)) plt.subplot(3,1,1) #拆分页面,多图展示 sns.distplot(data['SALARY_MILLIONS']) plt.xticks(np.linspace(0,40,9)) plt.ylabel(u'$Salary$',size=10) plt.subplot(3,1,2) sns.distplot(data['RPM']) plt.xticks(np.linspace(-10,10,9)) plt.ylabel(u'$RPM$',size=10) plt.subplot(3,1,3) sns.distplot(data['AGE']) plt.xticks(np.linspace(20,40,11)) plt.ylabel(u'$AGE$',size=10)
结果如下: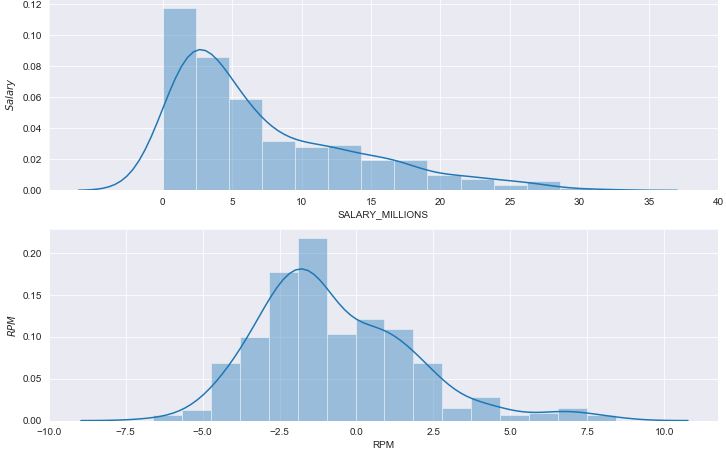
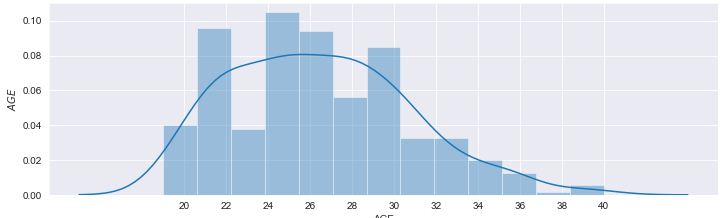
双变量:
dat1=data.loc[:,['RPM','SALARY_MILLIONS','AGE','POINTS']] sns.jointplot(dat1.SALARY_MILLIONS,dat1.AGE,kind='kde',size=8)
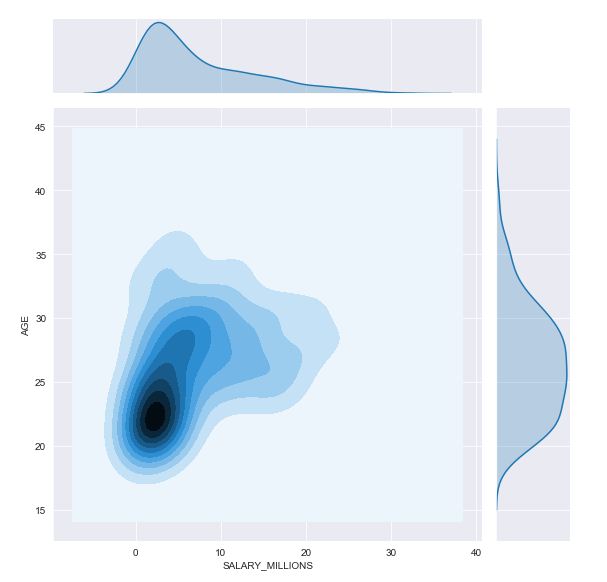
上图展示的是球员薪水与年龄的关系,采用不同的kind方式(等高线图/hex/散点等),我们可以整体感受一下年龄和薪水的集中特点,
大部分球员集中在22-25岁拿到5million以下的薪水,当然也有“年少成名”和“越老越妖”的情况。
多变量:
dat1=data.loc[:,['RPM','SALARY_MILLIONS','AGE','POINTS']] sns.pairplot(dat1) #相关性展示,斜对角为分布展示,可以直观地看变量是否具有现行关系


图展示的是球员薪水、效率值、年龄及场均得分四个变量间的两两相关关系,对角线展示的是本身的分布图,由散点的趋势我们可以看出不同特征的相关程度。
整体看各维度的相关性都不是很强,正负值与薪水和场均得分呈较弱的正相关性,
而年龄这一属性和其他的变量相关性较弱
